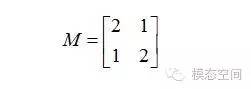奇異值分解(SVD)是線性代數中一種重要的矩陣分解方法,在數據壓縮存儲、搜索引擎、信號處理、統計學、動力學等領域有重要應用。在介紹奇異值分解之前,很有必要先介紹一下特征值分解。因為二者有著緊密的關聯,特征值分解和奇異值分解的目的都是一樣:提取出矩陣中最重要的特征。特征值和奇異值在大部分人的印象中,往往是停留在純粹的數學計算中。而且在線性代數或者矩陣論里面,也很少講任何跟特征值和奇異值有關的應用。奇異值分解是一個有著顯著物理意義的一種方法,它可以將一個比較復雜的矩陣用更小更簡單的幾個子矩陣的相乘來表示,這些小矩陣包含原始矩陣重要的特征。
特征值分解及其物理意義
對一個M×M的方陣A和向量υ,如果存在λ使得下式成立
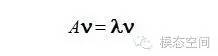 則稱λ為矩陣A的的特征值,υ稱為矩陣A的特征向量。一個矩陣的一組特征向量是一組正交向量。特征值分解是將一個矩陣分解成下面的形式
則稱λ為矩陣A的的特征值,υ稱為矩陣A的特征向量。一個矩陣的一組特征向量是一組正交向量。特征值分解是將一個矩陣分解成下面的形式
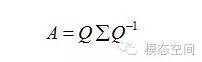 其中Q是這個矩陣A的特征向量組成的矩陣,Σ是一個對角陣,每一個對角線上的元素是一個特征值。首先,要明確的是,一個矩陣其實就是一個線性變換,因為一個矩陣乘以一個向量后得到的向量,其實就相當于將這個向量進行了線性變換。比如說下面的一個矩陣:
其中Q是這個矩陣A的特征向量組成的矩陣,Σ是一個對角陣,每一個對角線上的元素是一個特征值。首先,要明確的是,一個矩陣其實就是一個線性變換,因為一個矩陣乘以一個向量后得到的向量,其實就相當于將這個向量進行了線性變換。比如說下面的一個矩陣:
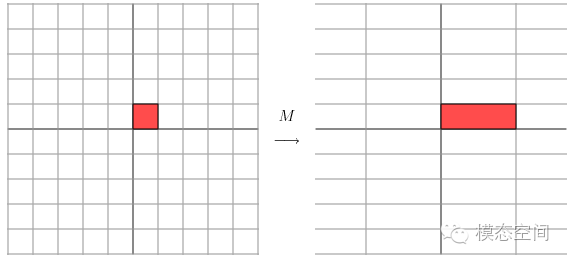
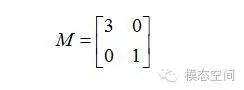 從幾何上來說,我們可以認為一個二維向量是幾何平面上的一點(x,y),通過矩陣M變換到另一點
從幾何上來說,我們可以認為一個二維向量是幾何平面上的一點(x,y),通過矩陣M變換到另一點
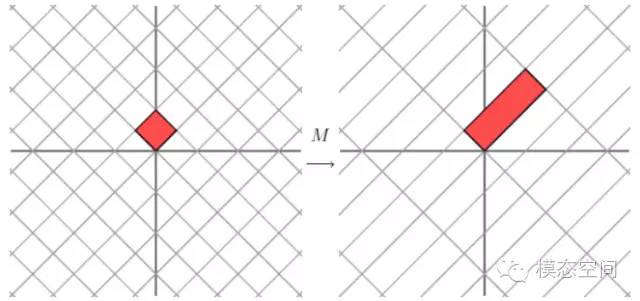
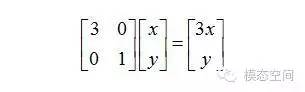 變換后的結果相當于乘以下圖所示的變換,即水平方向乘以了因子3(長度拉伸了3倍),垂直方向不變化。
變換后的結果相當于乘以下圖所示的變換,即水平方向乘以了因子3(長度拉伸了3倍),垂直方向不變化。
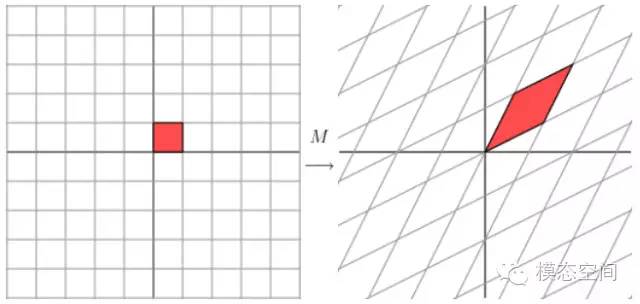 從上圖來看,簡單描述變換的幾何效果不是很容易。然而,讓我們將網格旋轉45度,再來看發生了什么。
從上圖來看,簡單描述變換的幾何效果不是很容易。然而,讓我們將網格旋轉45度,再來看發生了什么。
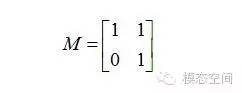 這個矩陣變換后得到的形狀為剪切形。
這個矩陣變換后得到的形狀為剪切形。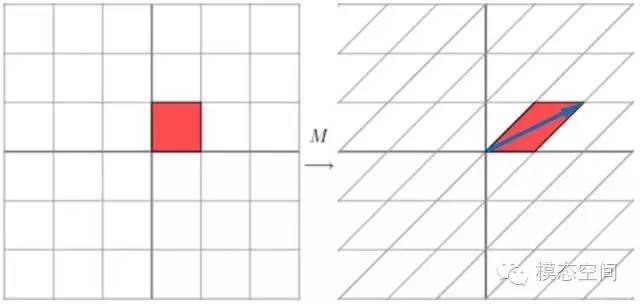 初看起來,這個網格不是正交的,但當對其旋轉58.28度之后,兩個網格都變成了正交網格。
初看起來,這個網格不是正交的,但當對其旋轉58.28度之后,兩個網格都變成了正交網格。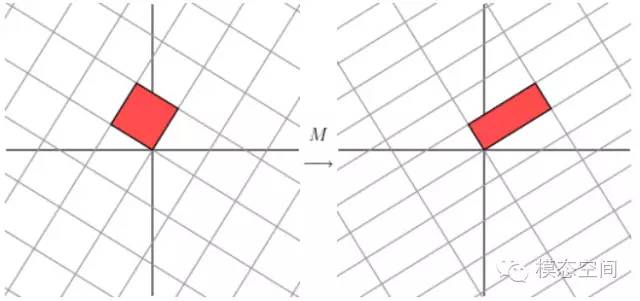
奇異值分解及其物理意義
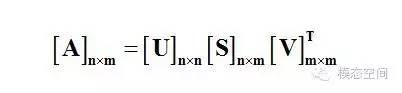 其中S=diag(σ1,σ2,……,σr),σi>0 (i=1,2…,r),r=rank(A)。得到的U是一個N×N的方陣(里面的向量是正交的,U里面的向量稱為左奇異向量)。S是一個N×M的矩陣(非對角線的元素都是0,對角線上的元素稱為奇異值),VT(是一個M×M的方陣,里面的向量也是正交的,V里面的向量稱為右奇異向量)。?在對矩陣進行奇異值分解時,是通過特征值分解方法求得的,首先將矩陣轉化為方陣,然后對其進行特征值分解。?假設對N×M的矩陣A進行奇異值分解,首先,我們將矩陣A左乘以它的轉置矩陣AT,將會得到一個M×M方陣,我們用這個方陣求特征值可以得到:
其中S=diag(σ1,σ2,……,σr),σi>0 (i=1,2…,r),r=rank(A)。得到的U是一個N×N的方陣(里面的向量是正交的,U里面的向量稱為左奇異向量)。S是一個N×M的矩陣(非對角線的元素都是0,對角線上的元素稱為奇異值),VT(是一個M×M的方陣,里面的向量也是正交的,V里面的向量稱為右奇異向量)。?在對矩陣進行奇異值分解時,是通過特征值分解方法求得的,首先將矩陣轉化為方陣,然后對其進行特征值分解。?假設對N×M的矩陣A進行奇異值分解,首先,我們將矩陣A左乘以它的轉置矩陣AT,將會得到一個M×M方陣,我們用這個方陣求特征值可以得到:
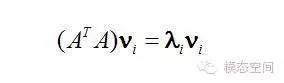 這里求得的υ就是上面的右奇異向量。?或者將我們將矩陣A右乘以它的轉置矩陣AT,將會得到一個N×N方陣,我們用這個方陣求特征值可以得到:
這里求得的υ就是上面的右奇異向量。?或者將我們將矩陣A右乘以它的轉置矩陣AT,將會得到一個N×N方陣,我們用這個方陣求特征值可以得到: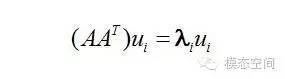
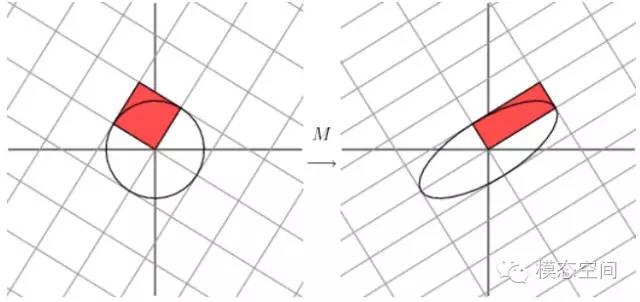
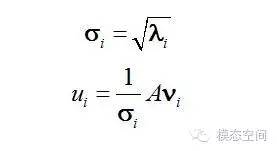 這里的σ就是上面所說的奇異值。u和υ分別是矩陣A的奇異向量,而S=diag(σ1,σ2,……,σr)是A的奇異值。AAT的正交單位特征向量組成U,特征值組成STS,ATA的正交單位特征向量組成V,特征值(與AAT相同)組成SST。也就是說,奇異值σ是矩陣特征值λ的非負平方根。因此,奇異值分解與特征值問題緊密相聯。
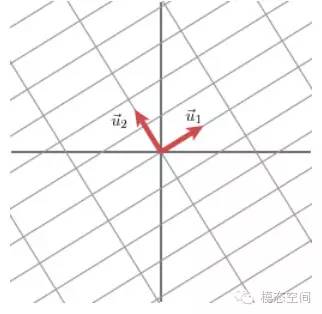
這里的σ就是上面所說的奇異值。u和υ分別是矩陣A的奇異向量,而S=diag(σ1,σ2,……,σr)是A的奇異值。AAT的正交單位特征向量組成U,特征值組成STS,ATA的正交單位特征向量組成V,特征值(與AAT相同)組成SST。也就是說,奇異值σ是矩陣特征值λ的非負平方根。因此,奇異值分解與特征值問題緊密相聯。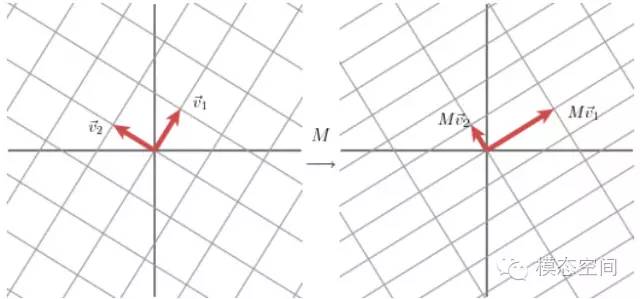 向量u1和u2表示Mv1和Mv2方向上的單位向量。Mv1和Mv2的長度,用σ1和σ2表示,這些數就是矩陣M的奇異值,它表示的是在這兩個特定的方向上網格被拉伸的幅度。
向量u1和u2表示Mv1和Mv2方向上的單位向量。Mv1和Mv2的長度,用σ1和σ2表示,這些數就是矩陣M的奇異值,它表示的是在這兩個特定的方向上網格被拉伸的幅度。
 我們有
我們有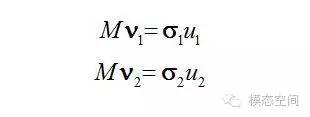
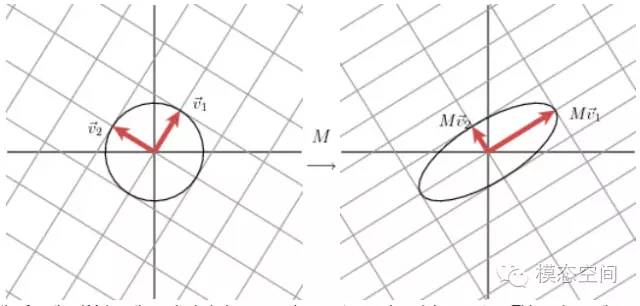 換句話說,單位圓上的|Mx|在v1方向上有最大值,在v2方向上有最小值。這樣就將問題簡化為相當標準的微積分問題:我們希望在整個單位圓上優化函數。結果是這個函數的關鍵點出現在矩陣MTM的特征向量處。既然這個矩陣是對稱陣,不同特征值對應的特征向量將是正交的。這些正交的向量是就vi。通過引入單位圓后的變換,我們就找到了變換后的主分量方向,即Mv1和Mv2方向,也就是向量u1和u2表示的方向。?
換句話說,單位圓上的|Mx|在v1方向上有最大值,在v2方向上有最小值。這樣就將問題簡化為相當標準的微積分問題:我們希望在整個單位圓上優化函數。結果是這個函數的關鍵點出現在矩陣MTM的特征向量處。既然這個矩陣是對稱陣,不同特征值對應的特征向量將是正交的。這些正交的向量是就vi。通過引入單位圓后的變換,我們就找到了變換后的主分量方向,即Mv1和Mv2方向,也就是向量u1和u2表示的方向。?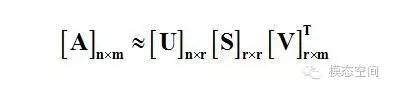
r是一個遠小于m、n的數。右邊的三個矩陣相乘的結果將會是一個接近于A的矩陣,在這兒,r越接近于m,則相乘的結果越接近于A。
奇異值分解與特征值分解的區別
轉自 譚祥軍? 《模態空間》