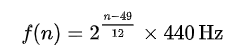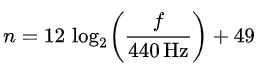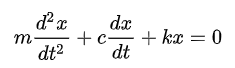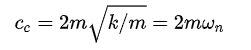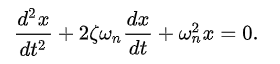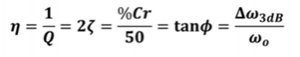The post 設置沖擊響應譜（SRS ）小波參數 appeared first on 杭州銳達數字技術有限公司.
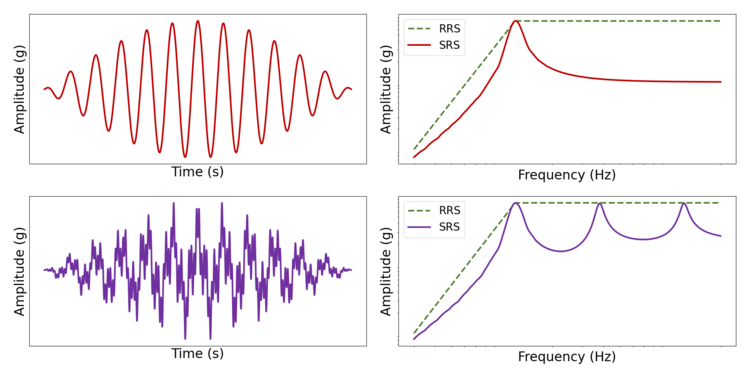
]]>- 沖擊響應譜是假設單自由度系統（彈簧上的單自由度又名質量）受到該脈沖時會發生什么的曲線圖
- X軸是該單自由度系統的固有頻率
- Y軸是單自由度響應中達到的最大相對加速度
- 用戶還必須提供阻尼比，因為單自由度響應需要阻尼和固有頻率
對于任何給定的沖擊波形，SRS可以通過迭代假設單自由度系統的固有頻率并繪制與固有頻率的最大響應來計算。還必須提供阻尼比（例如5%）來模擬單自由度系統。
從給定的SRS目標（也稱為所需反應譜或RRS）合成沖擊波形的相反方向不那么簡單，因為產生相同SRS的可能波形有無限多。
首先，需要注意的是，頻率為f的純正弦波會產生SRS，該SRS在響應譜域中的同一頻率f處急劇峰值。多個正弦波可以疊加在一起，產生一個組合的SRS，該SRS本質上是單個時間分量的相加。
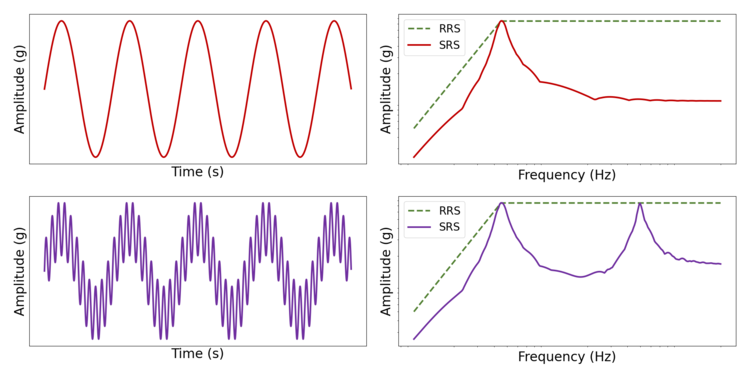因此，通過組合多個正弦小波，可以合成時間剖面脈沖以匹配給定的RRS。當單自由度系統主要以其固有頻率響應激勵時，每個小波負責激勵與其固有頻率對應的SRS值。
雖然可以使用直接正弦波，但更常見的是將正弦波窗口化為給定形狀，這也會影響最終合成小波的形狀。常用窗口包括正弦、漢寧和指數窗口。甚至可以根據用戶提供的錄制創建自定義窗口。
例如，下面是使用正弦窗口的正弦小波的公式和形狀：
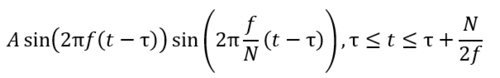
上圖中的頂部波形（紅色）是單個小波，而下面的波形是三個不同頻率的組合正弦小波的總和。請注意，所有三個頻率都反映在合成的SRS中。
采樣率是計算準確SRS信息的另一個重要方面。奈奎斯特規則規定，采樣率應至少是測量波形最大頻率含量的兩倍（在實踐中，使用接近2.56的系數）。
盡管所有頻率信息都是通過遵循奈奎斯特速率來捕獲的，但波形的實際時域表示并不那么準確，很可能會丟失信號的真實峰值。
MIL-STD-810建議使用的采樣率為測量波形最大頻率的10倍。這將準確捕獲波形峰值以計算SRS。
或者，如果采樣率至少滿足（~2.5 f）的奈奎斯特條件，則可以將信號重新采樣到更高的采樣率。當所有頻率信息都被捕獲時，可以通過以任意精度重新采樣來插值峰值。這可以通過時域中的零插值和低通濾波，或頻域中的零填充來實現。
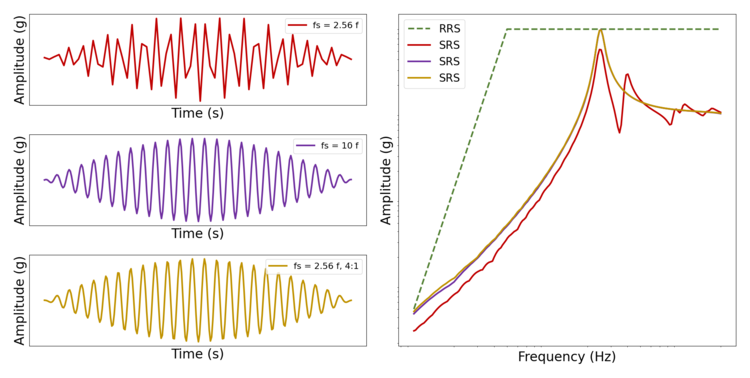上面是一個以奈奎斯特速率（紅色）采樣的正弦小波示例，與以10倍最大頻率（紫色）采樣的同一信號進行比較，最后是以奈奎斯特速率采樣的同一信號，然后以4:1的比率重新采樣。右邊的SRS圖顯示，直接10倍的采樣率或隨后的Nyquist比率重采樣足以準確捕獲SRS。
The post 設置沖擊響應譜（SRS ）小波參數 appeared first on 杭州銳達數字技術有限公司.
]]>The post 晶鉆專利：多分辨率頻譜分析在模態分析和振動控制的應用 appeared first on 杭州銳達數字技術有限公司.
]]>杭州銳達數字技術有限公司提供翻譯
前言
2019年7月，美國專利局批準了美國晶鉆儀器公司的一項發明專利，該項專利把多分辨頻譜分析技術用于模態分析和其他振動分析和控制領域。發明人 是晶鉆儀器公司的創始人James Zhuge 博士和 Jeff Zhao 博士，美國專利局申請號 15/668,995。本文是關于該發明的一部分描述和幾個具體應用。
機械結構和聲學應用中的很多問題要求譜分析采用非均勻的頻率分辨率。在這些應用中，我們更傾向于用對數刻度來描述頻率軸，由此低頻段有比高頻段更高的頻率分辨率。在介紹之后我們會討論一些例子。
在CI產品描述0001《動態信號分析技術》[2]中，我們討論了各種頻譜是如何計算的，包括線性譜、自譜、互譜、相位譜、相關函數和頻率響應函數。在現代動態信號分析儀產品中，這些譜都是通過Cooley-Tukey FFT算法計算的[1]。
離散傅里葉變換（DFT）的基本公式：
其中，
x(n) 時域波形樣本
n 樣本下標
N 樣本總數
k 有限分析頻率，對應FFT中心
X(k) x(n)的離散傅里葉變換形式
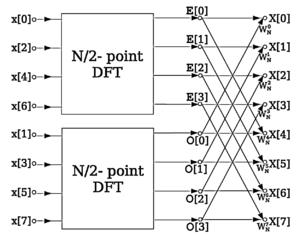
在多數情況下，我們采用基數為2的FFT算法，要求樣本總數是2的整數冪。
圖1 FFT算法結構的一個例子
FFT的一個顯著特點是將采樣率均勻的時域信號轉換成頻域信號會在整個頻率范圍內產生均勻的頻率分辨率。頻率分辨率dF，是時域塊信號的時長和塊大小N乘積的倒數。比如，將FFT應用到時長0.5s、塊大小N=1024的時域塊信號，那么頻率分辨率為1/(0.5 sec * 1024) = 0.001953125 Hz。
時域信號經FFT變換后，頻譜的頻率分辨率在分析頻率范圍內應均勻分布。10Hz處的頻率分辨率和1000Hz處的頻率分辨率相等。當分析中要求采用非均勻分布的頻率分辨率時，基于FFT的譜分析就不適用了。
DFT計算次數的量級是N*N，FFT計算次數的量級是NlogN，其中N是時域信號的塊大小。如果1965年Cooley和Tukey沒有發明出FFT算法，人們會使用效率較低的離散傅里葉變換（DFT）算法進行譜分析。DFT的優點是頻譜的分辨率不必均勻分布。實際上，在做DFT變換時，頻率分辨率可以任意分布，從這一點看DFT算法似乎優于FFT算法，然而DFT的計算花費太高了。
如果我們能夠找到一種計算效率和FFT一樣高，并且可以使頻譜的分辨率非線性分布（尤其是對數分布）的算法，將會是革命性的。
經過20多年的研發，晶鉆儀器公司成功將多分辨率頻譜分析方法引入并應用到其多個產品中，包括CI隨機振動控制器、動態信號分析儀和模態分析軟件。多分辨率頻譜分析方法解決上述提到的問題并具有一系列的優點，這篇文章將討論它的應用和結果。
要求采用非均勻頻率分辨率的例子
在這一節，我們討論幾個要求采用非均勻頻率分辨率的例子。
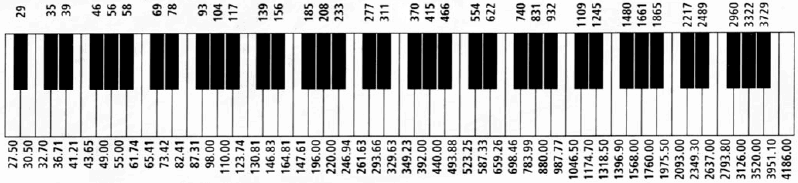
音樂頻率
鋼琴鍵盤上不同音調的頻率不是沿線性尺度均勻分布，而是沿對數尺度均勻分布。
其他樂器的音調具有和鋼琴相似的頻率分布。人們根據頻率來區分所聽到聲音的音調，這在對數尺度上很容易描述。
第n個鍵的頻率的計算公式如下：
（a’=A4=A440是標準鋼琴的第49個鍵）
上式可以寫成：
反過來，從標準鋼琴頻率440Hz開始，可以用如下公式計算鋼琴的鍵號：
用戶希望使用動態信號分析儀采集鋼琴聲音的時域信號，并對不同的聲調進行精確分析。由于人們聽到兩個聲調的區別主要是由兩個頻率大小的比率而不是兩個頻率大小的差引起的，那么就要求27.5Hz處的頻率分辨率比1760Hz處的高。如果頻譜分析儀在分析頻率范圍內分辨率都為1Hz，那么1760Hz的頻率讀數誤差小于0.1%，而27.5Hz的誤差可高達3%。這個例子告訴我們，設計一個可以提供頻率分辨率沿對數尺度均勻分布，而不是像FFT一樣沿線性尺度均勻分布的信號分析儀，將會是更好的解決方案。
共振頻率的阻尼估計
結構的動力學方程是
對應的臨界阻尼系數為
或者寫為
其中
是結構的固有頻率。
利用固有頻率和阻尼比的定義，可以把動力學方程寫成
阻尼比是無量綱的。
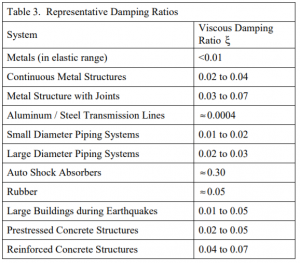
阻尼是結構動力學特性的主要因素。阻尼比ζ決定共振的強度，可以通過頻響函數測幅值計算得到。結構的阻尼比主要由材料決定，例如塑料的阻尼比比鋼要高得多。換句話說，給定材料的阻尼比通常在一定范圍內。
下表是幾種材料的粘性阻尼比[3]:
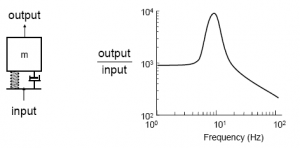
現在我們來看看如何用FFT信號分析儀來評估結構的阻尼比。利用FFT信號分析儀，可以計算出響應和激勵之間的頻響函數（FRF）。通常響應由安裝在結構上的加速度傳感器測得，激勵是力錘或振動臺對結構施加的力。
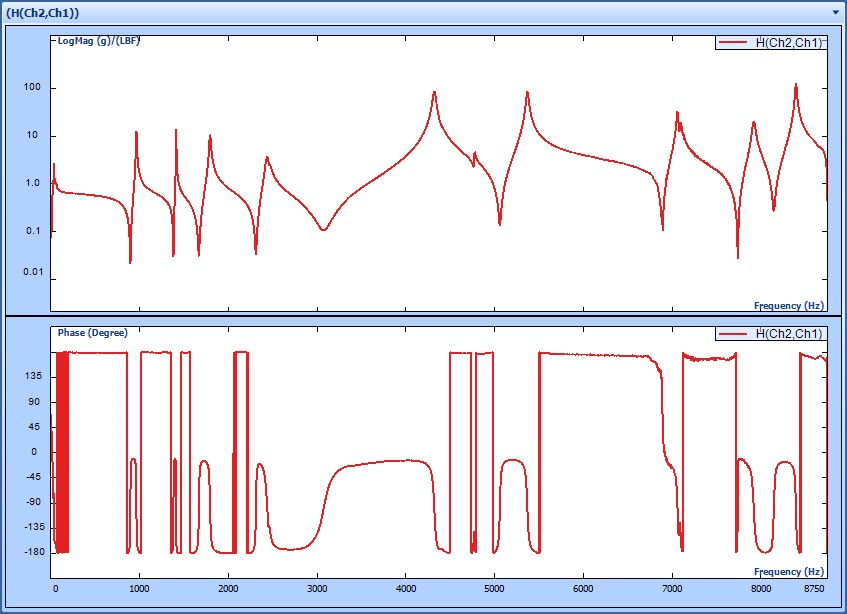
FRF可以通過文獻2中的方法計算得到。一個典型的FRF波德圖如下：
一種確定阻尼比的方法是在頻響函數共振頻率處采用“3dB法”，也稱“半功率法”。阻尼和FRF共振峰峰值往下取3dB左右兩邊的頻率寬度成正比。
通過公式Q = f0/(f2-f1)求得阻尼因子，其中
f0 共振峰頻率
f2 共振峰往下取3dB右側所對應的頻率
f1 共振峰往下取3dB左側所對應的頻率
衰減因子
Q 阻尼因子
ζ 阻尼比
%Cr 臨界阻尼百分數（%Cr=100%xζ）
? 周期應力和應變的相位角
為了計算阻尼因子Q = f0/(f2-f1)，需要確定三個頻率：FRF峰值所對應的頻率f0以及峰值下降3dB所對應的頻率f2和f1。頻率分辨率在計算中起關鍵作用，因為分辨率不足，計算出的Q值出現多個數量級的偏差的現象是很常見的。
對于特定的材料，其阻尼比ζ在一定的范圍內，頻譜分析要求在較低的共振頻率處具有更高分辨率。舉個例子，假設某種材料的阻尼比約為0.001，當共振頻率為1000Hz時，f2和f1處的頻率分辨率必須小于1Hz，當共振頻率為10Hz，f2和f1處的頻率分辨率必須小于0.01Hz。
振動臺振動控制
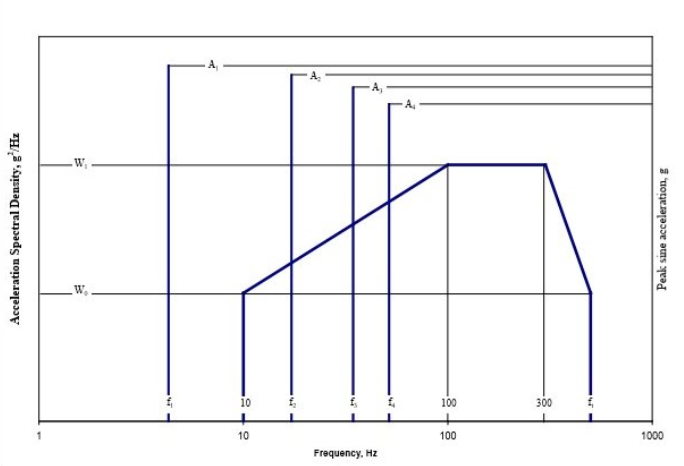
在許多振動控制測試中，頻率軸通常是用對數刻度而不是線性刻度繪制的。下面兩圖是Mil-810中典型的測試配置目標譜：
在介紹多分辨率頻譜分析法之前，我們知道目前市場上所有振動控制器都使用在分析頻率范圍內頻率分辨率均勻的FFT算法。換句話說，我們將多分辨率頻譜分析法應用到振動控制器上是史無前例的。
多分辨率頻譜分析介紹
由晶鉆儀器公司研發的多分辨率頻譜分析方法是對單通FFT的一種改進。它的基本原理是對相同的輸入時間流信號進行兩通或多通的FFT變換，然后在頻域中合成一個頻譜。下圖兩通FFT的工作示意圖：
當多個通道的時域信號輸入時，信號處理器將分塊接收，并通過FFT將時域塊信號轉換成頻域信號。同時，對原始時域信號應用濾波器，生成較低頻率的時域信號。FFT的第二通對較低頻率的時域信號使用較高分辨率的FFT變換，生成頻譜。最后，信號處理器將兩組頻譜綜合在一起，合成的頻譜有兩種不同的頻率分辨率，一種為dF，另一種為dF/M，其中M是采樣因子。
上面我們簡單地描述了多分辨率頻譜分析法的過程，然而實現起來是非常復雜的，有很多細節需要考慮，包括：
- 如何進行重疊處理?
- 使用哪種類型的濾波器，FIR還是IIR?
3.濾波器的濾波延時會有什么影響?
- 濾波器的相位畸變會有什么影響?
- 采樣因子從2、4、8中選取還是取其它的值?
- 如何將平均應用于多通FFT?
- 這種方法對什么類型的信號適用?對什么類型的信號不適用？
- 如何將數據窗口應用于多通時域信號?
晶鉆儀器公司的產品在應用多分辨率頻譜分析方法時，上述問題都得到了解決。產品軟件不僅可以進行多分辨率頻譜分析，還可以存儲數據、顯示結果和生成報告。
抽樣過程中生成連續的時間流信號，因此連續信號比瞬態信號更適合使用多分辨率頻譜分析法。例如，錘擊試驗通過產生瞬態信號來計算FRF，它就不適合使用多分辨率頻譜分析法。
將多分辨率頻譜分析法應用于結構振動分析。
多分辨率分析在模態分析的應用
我們通過一個模態試驗來比較多分辨率頻譜和單分辨率頻譜，模態分析軟件為晶鉆儀器自主研發的EDM Modal。被測結構是一塊鋼板，用彈簧繩垂直懸掛，以模擬自由邊界條件。用振動臺產生的白噪聲來激勵鋼板，用單軸加速度傳感器采集鋼板的響應信號。下面描述測試配置的詳細信息：采樣率51.2kHz，分析頻率范圍23kHz以內，塊大小4096，譜線數1800，頻率分辨率12.5Hz，通過漢寧窗減少信號泄露，用平均次數為32的線性平均模式來計算譜。利用多分辨率頻譜分析在低頻段獲得1.56Hz（12.5Hz的1/8）的分辨率。低頻段和高頻段的劃分頻率是2812.5Hz。在低頻段，由于分辨率提高，多分辨率譜的結果更好。在高頻段，多分辨率頻譜和單分辨率頻譜具有相同的頻率分辨率，因此得到相似的結果。多分辨率頻譜和單分辨率頻譜其它配置都相同。
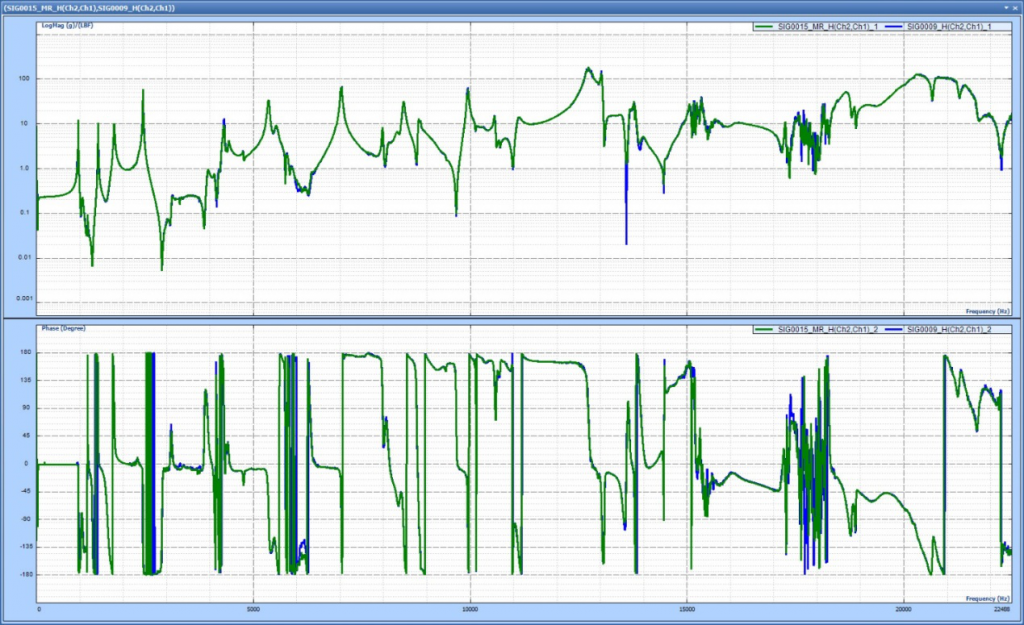
下圖是整個頻率范圍內的多分辨率譜和單分辨率譜：
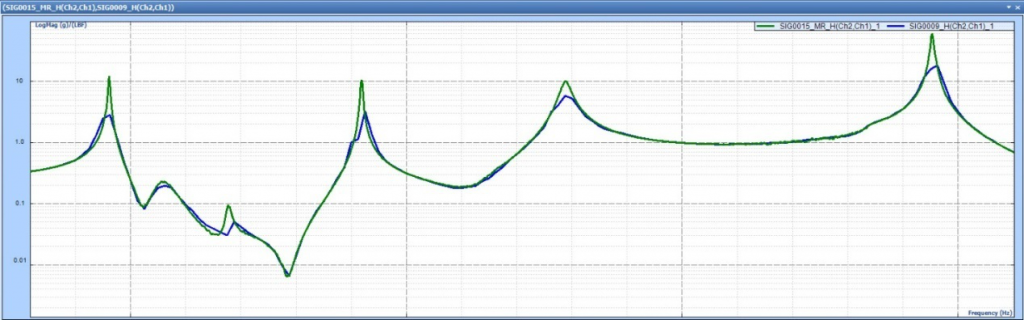
對多分辨率頻譜的高分辨率段進行放大，和單分辨率頻譜相比，得到如下頻譜圖：
在低頻段，多分辨率頻譜比單分辨率頻譜分辨率要高得多。從圖中可以看出，多分辨率頻譜由于塊大小更大、譜線數更多，峰值顯示更清晰。多分辨率頻譜比單分辨率頻譜的頻響函數曲線更光滑整潔。這有助于更好的計算FRF的質量因子和峰值。如下表所示，從表中可以看出，在低頻段出現四種共振頻率，在多分辨率頻譜下Q和FRF峰值要高很多。此外，在高頻段，由于單分辨率譜和多分辨率譜的分辨率是相同的，因此Q和FRF峰值也非常接近。常規FFT變換的Q和FRF峰值與真實值相差十個或數百個數量級，如果人們用這些錯誤的值進行分析，對結構進行優化，得出結果必然是錯誤的。
| Resonant Frequency | Q estimation using MR | Q estimation using regular FFT | FRF Amplitude Estimation using MR (g/LBF) | FRF Amplitude Estimation using regular FFT (g/LBF) |
| 960.94 Hz | 311.069 | 40.138 | 12.269 | 2.832 |
| 1418.75 Hz | 313.292 | 120.452 | 10.687 | 3.274 |
| 1789.06 Hz | 97.435 | 52.326 | 9.993 | 5.823 |
| 2453.13 Hz | 461.059 | 89.479 | 60.277 | 18.42 |
| 5350 Hz | 126.317 | 126.19 | 33.72 | 34.74 |
| 8462.5 Hz | 172.296 | 185.73 | 32.08 | 31.47 |
| 12725 Hz | 94.498 | 88.965 | 186.23 | 187.72 |
多分辨率分析在隨機振動控制的應用
將多分辨率頻譜分析方法進一步應用到振動測試控制系統中，這意味著將通過基于多分辨率頻譜分析方法的頻譜計算輸出信號。為了在保持合理的反饋控制時間內同時提高低頻段和高頻段的控制性能，可以在控制過程中對低頻段和高頻段應用不同的頻率分辨率。晶鉆儀器公司的隨機振動控制器產品將多分辨率頻譜分析法應用于計算所有功率譜、傳遞函數矩陣和振動臺的驅動信號。
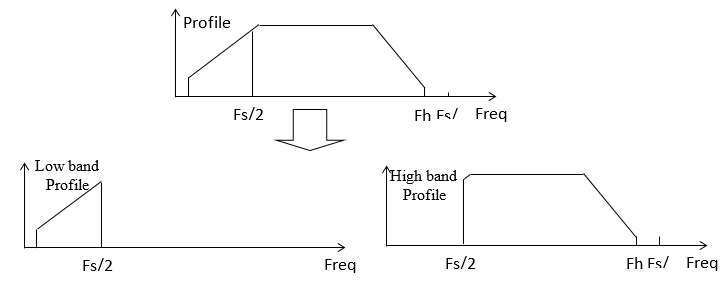
由于低頻段的驅動信號計算包含很多的細節，因此我們需要對低頻段使用更高的頻率分辨率。初始階段將用戶定義的目標譜分成高頻和低頻兩段。晶鉆儀器公司的Spider-81振動控制器將在這兩段目標譜上工作。
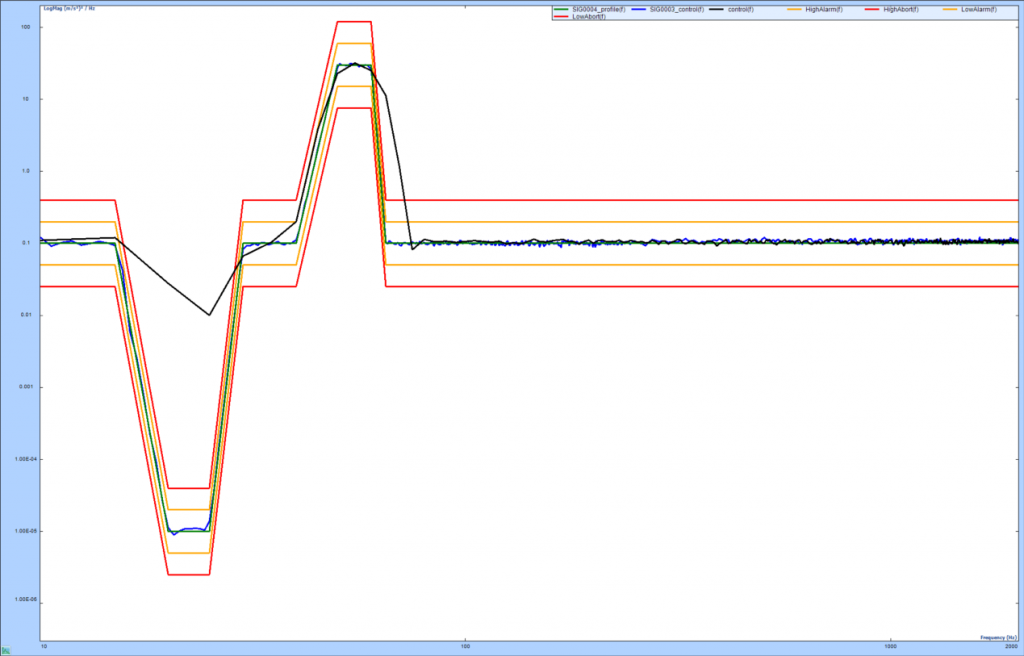
下面我們對單分辨率頻譜控制和多分辨率頻譜控制進行比較。下圖FFT譜線數為400，頻率范圍2kHz。單分辨率頻譜只有5Hz一種頻率分辨率，多分辨率頻譜低頻段分辨率為0.625Hz，高頻段分辨率為5Hz。圖中綠線為目標譜，黑線為單分辨率頻譜控制曲線，藍線是多分辨率頻譜控制曲線。
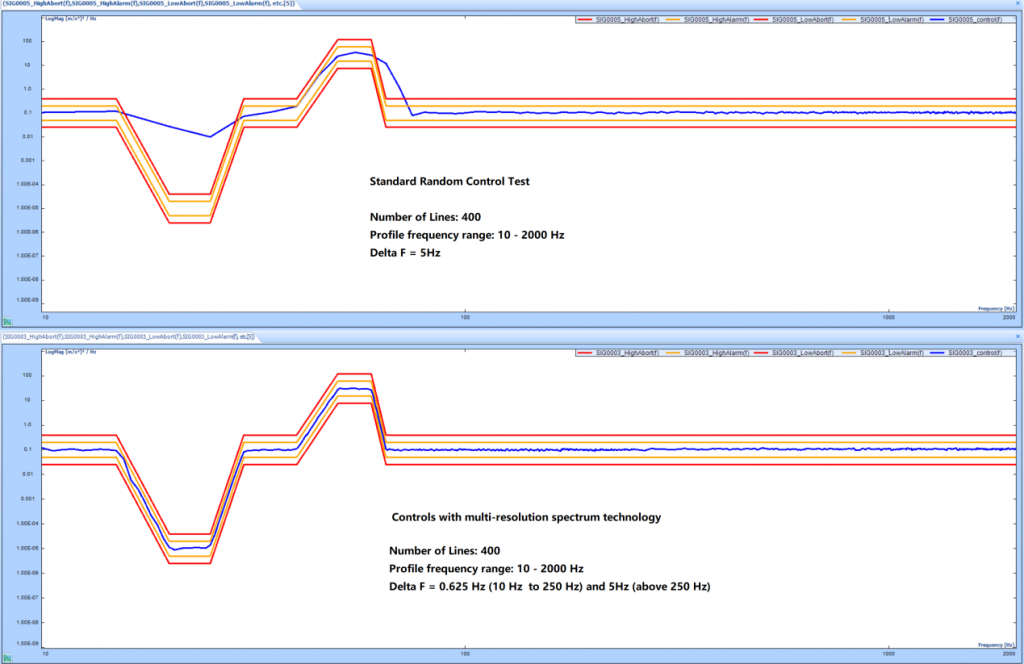
我們將單分辨率頻譜和多分辨率頻譜的控制曲線分開繪制。顯然，多分辨率頻譜比單分辨率頻譜控制得好。
結論
信號分析儀采用FFT算法對時域信號變換后，生成的頻譜只有均勻的頻率分辨率。然而，機械結構和聲學應用中的很多問題要求頻譜在低頻段有更高的頻率分辨率。由晶鉆儀器公司研發的多分辨率頻譜分析法可以將時域信號轉換成具有兩種以上的頻率分辨率的頻譜。該方法已經成功應用于隨機振動控制、動態信號分析和模態測試中，可以大大提高分析精度。
如果您對多分辨率分析功能想有更多的了解，歡迎咨詢杭州銳達數字技術有限公司，我們是晶鉆儀器公司在中國的總代理，為您提供技術咨詢、產品銷售、故障排除、產品維修等服務。
參考文獻
[1]. Cooley, James W.; Tukey, John W. (1965). “An algorithm for the machine calculation of complex Fourier series”. Mathematics of Computation. 19 (90): 297–301. doi:10.1090/S0025-5718-1965-0178586-1. ISSN 0025-5718.
[2]. Dynamic Signal Analysis Basics (Product Note #001, 32 pages, 1.1 MB, Crystal Instruments)
Describes the basic dynamic signal analysis theory including Fourier Transform, data windowing, linear spectrum, power spectrum, cross spectrum, FRF and coherence, averaging, transient capture and hammer test, overlapping process, SDOF system. Read online here.
[3]. V. Adams and A. Askenazi, Building Better Products with Finite Element Analysis, OnWord Press, Santa Fe, N.M., 1999.
The post 晶鉆專利：多分辨率頻譜分析在模態分析和振動控制的應用 appeared first on 杭州銳達數字技術有限公司.
]]>The post matlab數值積分的實現：時域積分和頻域積分 -轉載 appeared first on 杭州銳達數字技術有限公司.
]]>Double integration of raw acceleration data is a pretty poor estimate for displacement. The reason is that at each integration, you are compounding the noise in the data.
If you are dead set on working in the time-domain, the best results come from the following steps.
- Remove the mean from your sample (now have zero-mean sample)
- Integrate once to get velocity using some rule (trapezoidal, etc.)
- Remove the mean from the velocity
- Integrate again to get displacement.
- Remove the mean. Note, if you plot this, you will see drift over time.
- To eliminate (some to most) of the drift (trend), use a least squares fit (high degree depending on data) to determine polynomial coefficients.
- Remove the least squares polynomial function from your data.
A much better way to get displacement from acceleration data is to work in the frequency domain. To do this, follow these steps…
- Remove the mean from the accel. data
- Take the Fourier transform (FFT) of the accel. data.
- Convert the transformed accel. data to displacement data by dividing each element by -omega^2, where omega is the frequency band.
- Now take the inverse FFT to get back to the time-domain and scale your result.
This will give you a much better estimate of displacement.
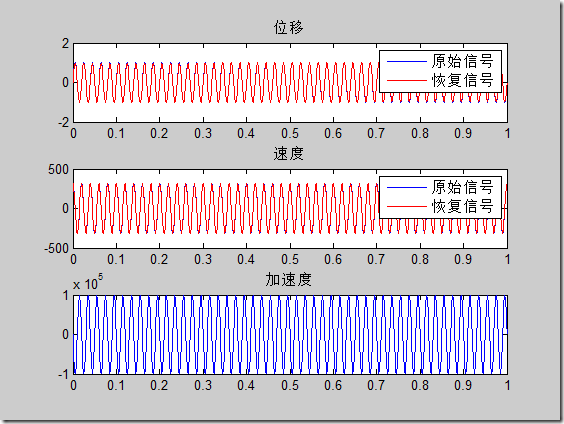
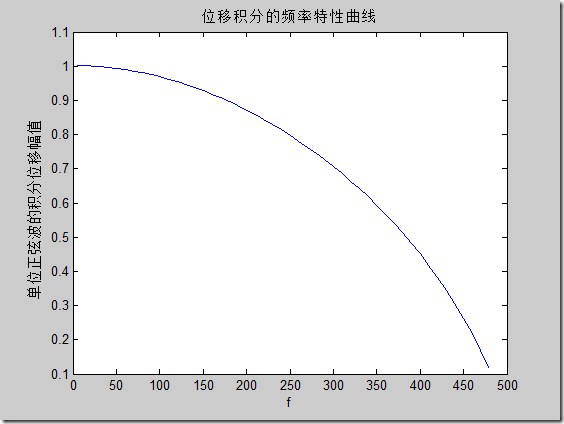
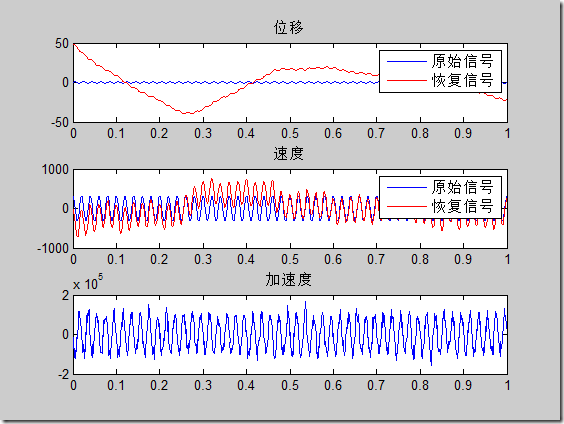
說到底就是頻域積分要比時域積分效果更好，實際測試也發現如此。原因可能是時域積分時積分一次就要去趨勢，去趨勢就會降低信號的能量，所以最后得到的結果常常比真實幅值要小。下面做一些測試，對一個正弦信號的二次微分做兩次積分，正弦頻率為50Hz，采樣頻率1000Hz，恢復效果如下：
時域積分
頻域積分
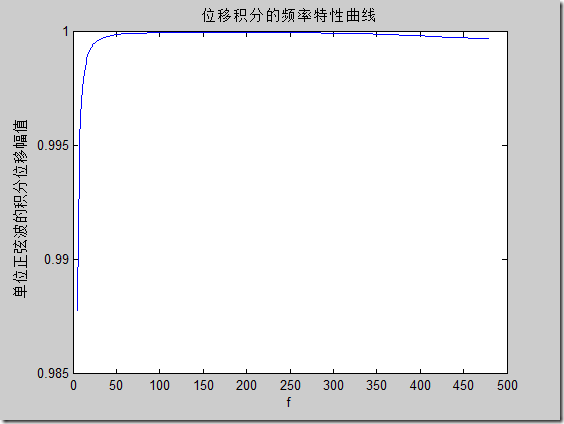
可見恢復信號都很好（對于50Hz是這樣的效果）。分析兩種方法的頻率特性曲線如下：
時域積分
頻域積分
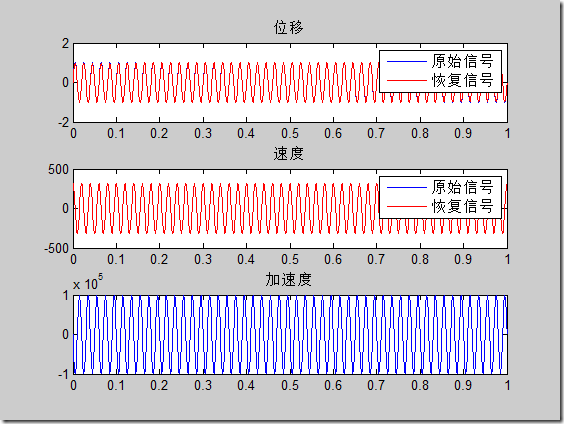
對于包含兩個正弦波的信號，頻域積分正常恢復信號，時域積分恢復的高頻信息有誤差；對于有噪聲的正弦信號，噪聲會使積分結果產生大的趨勢項（不是簡單的二次趨勢），如下圖：
對此可以用濾波的方法將大的趨勢項去掉。測試的代碼如下：
<section class="" data-source="bj.96weixin.com">
<blockquote class="">% 測試積分對正弦信號的作用
clc
clear
close all
% 原始正弦信號
ts = 0.001;
fs = 1/ts;
t = 0:ts:1000*ts;
f = 50;
dis = sin(2*pi*f*t);
% 位移
vel = 2*pi*f.*cos(2*pi*f*t);
% 速度
acc = -(2*pi*f).^2.*sin(2*pi*f*t);
% 加速度
% 多個正弦波的測試
% f1 = 400;
% dis1 = sin(2*pi*f1*t);
% 位移
% vel1 = 2*pi*f1.*cos(2*pi*f1*t);
% 速度
% acc1 = -(2*pi*f1).^2.*sin(2*pi*f1*t);
% 加速度
% dis = dis + dis1;
% vel = vel + vel1;
% acc = acc + acc1;
% 結：頻域積分正常恢復信號，時域積分恢復加入的高頻信息有誤差
% 加噪聲測試
acc = acc + (2*pi*f).^2*0.2*randn(size(acc));
% 結：噪聲會使積分結果產生大的趨勢項
figure
ax(1) = subplot(311);
plot(t, dis), title('位移')
ax(2) = subplot(312);
plot(t, vel), title('速度')
ax(3) = subplot(313);
plot(t, acc), title('加速度')
linkaxes(ax, 'x');
% 由加速度信號積分算位移
[disint, velint] = IntFcn(acc, t, ts, 2);
axes(ax(2));hold on
plot(t, velint, 'r'),
legend({'原始信號', '恢復信號'})
axes(ax(1));hold on
plot(t, disint, 'r'),
legend({'原始信號', '恢復信號'})
% 測試積分算子的頻率特性
n = 30;
amp = zeros(n, 1);
f = [5:30 40:10:480];
figure
for i = 1:length(f)
fi = f(i);
acc = -(2*pi*fi).^2.*sin(2*pi*fi*t);
% 加速度
[disint, velint] = IntFcn(acc, t, ts, 2);
% 積分算位移
amp(i) = sqrt(sum(disint.^2))/sqrt(sum(dis.^2));
plot(t, disint)
drawnow
end
close
figure
plot(f, amp)
title('位移積分的頻率特性曲線')
xlabel('f')
ylabel('單位正弦波的積分位移幅值')</blockquote>
</section>
以上代碼中使用IntFcn函數實現積分，它是封裝之后的函數，可以實現時域積分和頻域積分，其代碼如下：
<section class="" data-source="bj.96weixin.com">
<blockquote class="">% 積分操作由加速度求位移，可選時域積分和頻域積分
function [disint, velint] = IntFcn(acc, t, ts, flag)
if flag == 1
% 時域積分
[disint, velint] = IntFcn_Time(t, acc);
velenergy = sqrt(sum(velint.^2));
velint = detrend(velint);
velreenergy = sqrt(sum(velint.^2));
velint = velint/velreenergy*velenergy;
disenergy = sqrt(sum(disint.^2));
disint = detrend(disint);
disreenergy = sqrt(sum(disint.^2));
disint = disint/disreenergy*disenergy;
% 此操作是為了彌補去趨勢時能量的損失
% 去除位移中的二次項
p = polyfit(t, disint, 2);
disint = disint – polyval(p, t);
else
% 頻域積分
velint = ?iomega(acc, ts, 3, 2);
velint = detrend(velint);
disint = ?iomega(acc, ts, 3, 1);
% 去除位移中的二次項
p = polyfit(t, disint, 2);
disint = disint – polyval(p, t);
end
end</blockquote>
</section>
其中時域積分的子函數如下：
<section class="" data-source="bj.96weixin.com">
<blockquote class="">% 時域內梯形積分
function [xn, vn] = IntFcn_Time(t, an)
vn = cumtrapz(t, an);
vn = vn – repmat(mean(vn), size(vn,1), 1);
xn = cumtrapz(t, vn);
xn = xn – repmat(mean(xn), size(xn,1), 1);
end</blockquote>
</section>
頻域積分的子函數如下（此代碼是一個老外編的，在頻域內實現積分和微分操作）
<section class="" data-source="bj.96weixin.com">
<blockquote class="">function dataout = ?iomega(datain, dt, datain_type, dataout_type)
%%%%%%%%%%%%%%%%
%
% ? IOMEGA is a MATLAB script for converting displacement, velocity, or
% ? acceleration time-series to either displacement, velocity, or
% ? acceleration times-series. The script takes an array of waveform data
% ? (datain), transforms into the frequency-domain in order to more easily
% ? convert into desired output form, and then converts back into the time
% ? domain resulting in output (dataout) that is converted into the desired
% ? form.
%
% ? Variables:
% ? ———-
%
% ? datain ? ? ? = ? input waveform data of type datain_type
%
% ? dataout ? ? ?= ? output waveform data of type dataout_type
%
% ? dt ? ? ? ? ? = ? time increment (units of seconds per sample)
%
% ? ? ? ? ? ? ? ? ? ?1 – Displacement
% ? datain_type ?= ? 2 – Velocity
% ? ? ? ? ? ? ? ? ? ?3 – Acceleration
%
% ? ? ? ? ? ? ? ? ? ?1 – Displacement
% ? dataout_type = ? 2 – Velocity
% ? ? ? ? ? ? ? ? ? ?3 – Acceleration
%
%
%%%%%%%%%%%%%%%%
% ? Make sure that datain_type and dataout_type are either 1, 2 or 3
if (datain_type < 1 || datain_type > 3)
error('Value for datain_type must be a 1, 2 or 3');
elseif (dataout_type < 1 || dataout_type > 3)
error('Value for dataout_type must be a 1, 2 or 3');
end
% ? Determine Number of points (next power of 2), frequency increment
% ? and Nyquist frequency
N = 2^nextpow2(max(size(datain)));
df = 1/(N*dt);
Nyq = 1/(2*dt);
% ? Save frequency array
iomega_array = 1i*2*pi*(-Nyq : df : Nyq-df);
iomega_exp = dataout_type – datain_type;
% ? Pad datain array with zeros (if needed)
size1 = size(datain,1);
size2 = size(datain,2);
if (N-size1 ~= 0 && N-size2 ~= 0)
if size1 > size2
datain = vertcat(datain,zeros(N-size1,1));
else
datain = horzcat(datain,zeros(1,N-size2));
end
end
% ? Transform datain into frequency domain via FFT and shift output (A)
% ? so that zero-frequency amplitude is in the middle of the array
% ? (instead of the beginning)
A = fft(datain);
A = fftshift(A);
% ? Convert datain of type datain_type to type dataout_type
for j = 1 : N
if iomega_array(j) ~= 0
A(j) = A(j) * (iomega_array(j) ^ iomega_exp);
else
A(j) = complex(0.0,0.0);
end
end
% ? Shift new frequency-amplitude array back to MATLAB format and
% ? transform back into the time domain via the inverse FFT.
A = ifftshift(A);
datain = ifft(A);
% ? Remove zeros that were added to datain in order to pad to next
% ? biggerst power of 2 and return dataout.
if size1 > size2
dataout = real(datain(1:size1,size2));
else
dataout = real(datain(size1,1:size2));
end
return</blockquote>
</section>
杭州銳達微信二維碼
The post matlab數值積分的實現：時域積分和頻域積分 -轉載 appeared first on 杭州銳達數字技術有限公司.
]]>The post 動態信號分析儀的應用及原理 appeared first on 杭州銳達數字技術有限公司.
]]>目前各國生產的動態信號分析儀型號規格很多性能也各異，如美國晶鉆儀器公司的CoCo80和CoCo90動態信號分析儀，它是一款便攜式儀器，同時具有數據動態數據記錄功能，它有4/8/16輸入通道，最高采樣率102.4KHz，最高150dB的動態范圍，數字濾波器有效防止削波等，自帶電池與內存，特別適合野外實時數據采集與分析，在橋架結構監測、大型機械狀態監測、高校振動試驗、汽車NVH模態分析、航空航天高鐵隧道監測、環境噪聲監測、聲學分析等，功能有頻譜分析及相關函數、結構模態分析、動平衡、路徑采集點檢、旋轉機械階次跟蹤、倍頻程和聲級計、全身振動、閾值檢測、沖擊響應譜和正弦掃頻、包絡分析、數據采集等。
動態信號分析儀原理
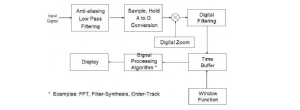
動態信號分析儀一般由如下幾個部分組成：?1）防混疊低通濾波器；?2）模擬到數字轉換器ADC； 3）數字信號處理器：數字變頻，數字濾波，數字信號處理（如FFT等頻率分析函數）等；?4）控制和顯示
The post 動態信號分析儀的應用及原理 appeared first on 杭州銳達數字技術有限公司.
]]>The post Me’Scope軟件支持的數據格式有哪些？ appeared first on 杭州銳達數字技術有限公司.
]]>
Me’Scope軟件支持的數據格式有哪些？
軟件支持數據格式
Me’Scope軟件支持從大多數常見采集儀，分析儀直接導入數據。通用格式 ● ASCII Spreadsheet ● Matlab version 4 ●
通用格式
● ASCII Spreadsheet
● Matlab version 4
● Microsoft WAV
● Universal File Format (UFF) Dataset 58 – supported by many Analyzers/Recorders
● Binary Universal File Format (BUFF) Dataset 58b? – supported by many Analyzers/Recorders
支持的分析儀/記錄儀（或者查看硬件支持列表）
● A&D World Class Analyzer
● Advantest R-9211
● Agilent Technologies (Hewlett Packard Standard Data format)
● Brüel & Kj?r
-Models 214x, 2260 and 3550
-Dactron RT-Pro saves data in ME’scope format
-Pulse
● Bridge Diagnostics
● B-S Multidata
● Cognitive Vision CV-390,395 XRC format
● Commtest – Saves data in Universal File (UFF) format
● DASYLab
● Data Physics
-SignalCalc software saves data in ME’scope format
● Dewetron saves data in Universal File (UFF) format
● DLI Instruments – Watchman saves data in UFF format
● DSP Development – DADiSP
● Emerson Process Management (CSI)
-RBMware/AMS Suite – The Advanced Vibration module (VibPro) saves FRFs in ME’scope format
● FAMOS
● HEAD acoustics – ArtemiS saves data in ME’scope format and Universal File (UFF) format
● Hioki Recorders
● Hewlett Packard Standard Data Format
● IO Tech – ez-Analyst software saves data in ME’scope format
● Larson Davis 2800/2900/3000/3200
● LMS International – saves data in Universal File (UFF) format
● Mathworks – Matlab Utility?to save data in Universal File (UFF) format
● Müller BBM – PAK saves data in ME’scope format
● National Instruments
-ez-Analyst software saves data in ME’scope format
-LabView Sound and Vibration Toolkit saves data in Universal File (UFF) format
● OnoSokki
-Binary (*.DAT) file format for newer analyzers
-ASCII/Binary Intensity data formats
-ORF Format
● Oros
-OR 3 Series RES and OXF files
-OR 2 Series AE2 files
● Polytec/PI – Scanning vibrometers save data in ME’scope format
● DLI Engineering – Signal AQ saves data in Universal File (UFF) format
● SKF Condition Monitoring
-Microlog MX
-Peak and Phase import from CMXA-50
● Sony Recorders – PCscan format
● Spectral Dynamics – ME’scope imports Star data and UFF format data
● Teac Recorders
-TAFF MAT
-QuikVu format import
結構/有限元軟件
● Ansys – RST, CDB formats
● AutoDesk
-AutoCAD DXF
-3DS Max
● NASTRAN – Bulk Data/F06 (Mode Shapes)
● SDRC
-FEMAP Neutral Files
-I-Deas Universal File Format
● STL (Stereo Lithography) Format – ASCII/Binary
● Wavefront OBJ
The post Me’Scope軟件支持的數據格式有哪些？ appeared first on 杭州銳達數字技術有限公司.
]]>The post Me’Scope結構動力學與聲學功能模塊 appeared first on 杭州銳達數字技術有限公司.
]]>? ? ?VT-540在VT-570模態分析軟件包基礎上增加了VES-5000結構動力學修改選項。
VT-560在VT550高級模態分析軟件包基礎上增加了VES-5000結構動力學修改選項。
利用模態分析可以找到機械或結構的問題，當進一步想要解決問題時就需要用更多分析手段。結構動力學修改軟件包有助于解決結構共振問題，能夠找到結構修改與動力學變化之間的關系，有效地幫助用戶優化結構設計。
增加的功能：
–?結構修改
–?模態靈敏度分析
–?附屬結構
–?已知修改帶來的振形尺度
–?各種單元的選擇
–?質量，彈簧，阻尼單元
–?梁，桿單元
–?三角形，方形面單元
–?多面體單元
–?調諧隔振單元
Me’Scope聲學功能模塊VT-710 Visual Acoustics
VT-710在VT-620基本軟件包基礎上增加了VES-6000聲學分析選項。能夠將聲音信號進行處理并顯示，如聲強，聲壓級，聲功率，倍頻程，窄帶數據。允許同時將振動信號和聲音信號顯示在一起。
特點：
–?動畫顯示聲學和振動信號
–?顯示窄頻段，1/1，1/3，1/12，1/24 倍頻程的測量數據
–?用互功率譜或時域數據計算聲強
–?由聲強數據計算通過表面的聲音功率
–?把窄頻段數據轉換成倍頻程
–?對窄頻段數據，倍頻程進行A,B,C 加權
–?噪聲源以百分比，分貝或瓦特分級
–?幅值和相位單音標定
The post Me’Scope結構動力學與聲學功能模塊 appeared first on 杭州銳達數字技術有限公司.
]]>The post Me’Scope高級模態分析模塊VT-550 Visual Modal Pro功能 appeared first on 杭州銳達數字技術有限公司.
]]>高級模態分析提供了更多的高級曲線擬合方法，能夠更精確地區分出重模態或相近模態。它還包含了高級信號處理功能比如MIMO分析，能夠從采集的原始數據中計算獲得多參考FRFs。
舉例：有一個橋梁實驗用的是多激振器激勵測試方法，現場只采集了時域的力和振動信號，通過ME’scope的高級模態分析功能后處理計算得到多參考FRFs，從而能夠進一步的實現模態分析。模態結果如右圖所示。
特點：
–?MDOF Z-多項式曲線擬合
– MDOF?復指數曲線擬合
– MDOF ERA?曲線擬合
– 多參考曲線擬合
– 穩定性圖解。在一定曲線擬合范圍內顯示頻率和阻尼
– 復模態式指示函數（CMIF）
– 多模態指示函數（MMIF）
– 模態置信標準（MAC），數字形態比較
– 采用MIMO FRF 矩陣計算結構響應，頻響函數或激振力
The post Me’Scope高級模態分析模塊VT-550 Visual Modal Pro功能 appeared first on 杭州銳達數字技術有限公司.
]]>The post Me’Scope模態分析模塊VT-570 Visual Modal和高級ODS軟件包VT-420 Visual ODS Pro appeared first on 杭州銳達數字技術有限公司.
]]>該模塊包含了Visual ODS Pro和VES-4000選項，能夠從實驗數據中識別出頻率，阻尼和振形。
特點：
– SDOF Co-Quad & Peak?曲線擬合方法
–?MDOF?多項式曲線擬合方法，對超頻段進行補償。
–?局部和全局曲線擬合
–?快速擬合命令，擬合一步到位
–?對選取的測量數據段進行交互曲線擬合
–?模態指示函數可用于共振峰個數計數
–?在模態指示圖形上重疊顯示估計的頻率和阻尼
–?使用模態參數進行頻響函數合成
–?所有曲線擬合函數和模態參數與各數據塊一起存儲
–?模態參數以UFF 格式輸入輸出
高級ODS軟件包VT-420 Visual ODS Pro
Visual ODS Pro包含Visual ODS和VES-3000信號處理選項。
增加的功能：
–?FFT和IFFT功能
–?時/頻信號的積分和微分變換
–?波形剪切，拷貝和粘貼
– 凹槽/帶通窗去除不必要的數據
– 指數窗去除噪聲或使波峰更尖銳
–?全局/帶選能量，平均能量計算
–?自/互譜，PSDs，ODS FRFs計算
–?階次跟蹤ODS顯示
The post Me’Scope模態分析模塊VT-570 Visual Modal和高級ODS軟件包VT-420 Visual ODS Pro appeared first on 杭州銳達數字技術有限公司.
]]>The post ME’scopeVES模態分析基本模塊VT-620 Visual ODS功能 appeared first on 杭州銳達數字技術有限公司.
]]>Visual ODS從大量的時域和頻域信號中提取出機械或結構的運動規律。如圖所示的一個案例中，一臺安裝在樓頂的皮帶驅動鼓風機工作不正常，有很大的振動和噪聲，嘗 試過做風扇葉片動平衡并未解決問題。利用現場采集到的一組轉速信號和一組振動信號進行ODS分析發現，電機端基礎與電機振動相位有差異，現場刮出油漆后發 現了隱藏的裂紋。修復裂紋后振動噪聲問題得到了有效地解決。
– 交互式3D結構建模
–?繪圖助手更有效地提高建模效率，內建3D模型可供調用
–?模型尺寸，形狀，位置，坐標系等都可直觀地更改
–?4視角同時顯示（X，Y，Z，自定義）
–?放大縮小，旋轉等操作簡單明了
–?可剪切，復制，粘貼繪圖對象
–?點坐標信息可直接從表格中復制獲得
–?2D模型可以從數碼照片中描繪
–?每個3D模型部件都可以定義不同的坐標系以匹配測量坐標系
–?模型可以從其他軟件中導入，如UFF，AutoCAD，有限元軟件
–?模型尺寸沒有限制
時域和頻域數據
–?數據可以從通用的采集儀，記錄儀中導入
–?支持大多數數據格式
–?導入的數據沒有大小和數量限制
–?數據可以顯示為實部，虛部，幅值，相位，Bode，Nyquist，Orbit等形式
–?多組數據可以組成重疊圖，瀑布圖，色彩圖
–?多種光標可選
–?圖表可以保存為常用圖片格式
ODS動畫
–?通過調節光標來實現交互式掃描，駐留或靜態動畫顯示
–?自動將沒有數據的模型點關聯到相近的數據點
–?不同信號源之間的動畫比較
–?多種動畫顯示方式，變形，箭頭，輪廓，色彩
–?動畫軌跡圖顯示
–?隱藏線顯示（虛線或隱藏）
–?模型表面著色
–?生成AVI動畫視頻
The post ME’scopeVES模態分析基本模塊VT-620 Visual ODS功能 appeared first on 杭州銳達數字技術有限公司.
]]>The post ME’scopeVES軟件功能選項有那些？ appeared first on 杭州銳達數字技術有限公司.
]]>| Signal Processing信號處理 | 控制用戶硬件采集獲取數據并進行預處理，包括FFT和IFFT，自譜和互譜，PSDs，ODS FRFs等 |
| Visual ODS(Pro)工作變形分析 | 交互式動態顯示被測物體的實際工作形態（ODS）、模態、聲學分布形態和工程數據的形態等 |
| Visual Modal(Pro)模態分析 | 從實驗數據中識別模態頻率，阻尼和振形；提供多種曲線擬合方式來優化模態結果 |
| Visual OMA工作模態分析 | 無激勵信號條件下的模態分析，直接從特殊處理的互譜或ODS FRFs數據中提取出模態參數 |
| Visual SDM(Pro)結構動力學修改 | 在模型結構上增加如質量，彈性，梁，板等單元以改變結構共振點，達到結構優化設計的目的 |
| Visual Acoustics(Pro)聲學模塊 | 處理并顯示聲強度，聲壓級，聲功率，倍頻程等數據，能同時顯示聲學和振動信號 |
| Visual experimental FEA有限元分析 | 將實驗數據與有限元分析進行結合，有限元模型可導入導出到其他有限元分析軟件中 |
| Visual FEA Modal Updating模態更新 | 利用實驗結果修正有限元模型，可修改參數包括：彈性，質量，阻尼，桿，梁，面單元以及材料屬性 |
信號處理選項VES-3000 Signal Processing
Me’Scope VES-3000包含了FFT和IFFT功能，不論你采集的數據是時域還是頻域都可以轉換成模態分析所需要的數據。它還包含了加窗功能，可以精確地選擇理想數據，濾除不需要的部分。它還包含了波形剪切，復制，粘貼，積分，微分等變換功能。
信號計算包括：FFT，自/互譜，PSDs，ODS FRF，其中ODS FRFs可以用作工作變形分析和工作模態分析。
特點：
– FFT和IFFT功能
–?時/頻信號的積分和微分變換
–?波形剪切，拷貝和粘貼
–?凹槽/帶通窗去除不必要的數據
–?指數窗去除噪聲或使波峰更尖銳
–?全局/帶選能量，平均能量計算
–?自/互譜，PSDs，ODS FRFs計算
–?階次跟蹤ODS顯示
MIMO建模和仿真選項VES-3500 MIMO Modeling & Simulation
VES-3550選項適用于多點激勵情況，利用多輸入多輸出(MIMO)矩陣計算多點激勵情況下的系統響應。能夠計算得到MIMO FRFs,多點或部分相干函數。
基本模態分析選項VES-4000 Modal Analysis
VES-4000選項通過對大量FRFs的曲線擬合能夠估算出模態參數(頻率，阻尼和振形)。它包含多種模態指示函數以及多種曲線擬合方法，來有效地識別各階模態。
特點：
–?SDOF Co-Quad and Peak擬合方法
–?MDOF Rational Fraction Polynomial擬合方法
–?工作模態曲線擬合
–?一鍵快速MDOF擬合
–?模態指示函數
–?從模態參數中合成FRFs
高級模態分析選項VES-4500 Multi-Reference Modal Analysis
該選項提供了更多的曲線擬合方法，多種多參考擬合方法能夠有效地識別重合或者相近模態。它還包含了穩態圖，極點圖，模態置信度準則(MAC)等功能。
特點：
–?MDOF復指數時域擬合方法
–?MDOF Z-Polynomial (LSCF)擬合方法
–?MDOF Alias Free Polynomial (AF Poly)擬合方法
–?多參考點曲線擬合
–?復模態式指示函數（CMIF）,多模態指示函數（MMIF）
–?穩態圖，MAC and CoMAC示圖，Manhattan示圖
工作模態選項VES-4700 Operating Modal Analysis
選項適用于無法測量獲得激勵信號或只有響應信號情況下的模態分析。通過分析特殊處理的互譜或者ODS FRFs來進行模態識別。
結構動力學修改選項VES-5000 Structural Dynamics Modifications
VES-5000選項能夠模擬對結構進行改動帶來的動力學改變。結構改變包括：增加彈簧，質量，阻尼，梁，桿，板，體等單元。也可以在結構上增加特定的調諧隔振單元或者附屬結構來研究動力學問題。
特點：
–?結構修改
–?模態靈敏度分析
–?附屬結構
–?已知修改帶來的振形尺度
–?各種單元的選擇
–?質量，彈簧，阻尼單元
–?梁，桿單元
–?三角形，方形面單元
–?多面體單元
–?調諧隔振單元
聲學分析選項VES-6000 Acoustics
VES-6000選項能夠將聲音信號進行處理并顯示，如聲強，聲壓級，聲功率，倍頻程，窄帶數據。允許同時將振動信號和聲音信號顯示在一起。
特點：
–?動畫顯示聲學和振動信號
–?顯示窄頻段，1/1，1/3，1/12，1/24 倍頻程的測量數據
–?用互功率譜或時域數據計算聲強
–?由聲強數據計算通過表面的聲音功率
–?把窄頻段數據轉換成倍頻程
–?對窄頻段數據，倍頻程進行A,B,C 加權
–?噪聲源以百分比，分貝或瓦特分級
–?幅值和相位單音標定
有限元選項VES-8000 Finite Element Analysis (FEA) Option
VES-8000選項能夠利用有限元模型計算得到模態結果，包含各種典型的有限元單元。你可以快速地利用已有有限元模型進行實驗模型建模。將有限元分析與實驗數據有機結合。有限元模型可以導入導出到通用過的有限元分析軟件中。
模態更新選項VES-9000 FEA Model Updating Option
VES-9000選項利用實驗結果修正有限元模型，可修改參數包括：彈性，質量，阻尼，桿，梁，面單元以及材料屬性。
The post ME’scopeVES軟件功能選項有那些？ appeared first on 杭州銳達數字技術有限公司.
]]>